What are radians? A simple explanation of radian vs. degree
Are you ready to take your academic journey to the next level? We've got just the thing for you: UPchieve, your ultimate homework help companion! Sign up today for free!
Introduction
If you’re new to trigonometry, you may be hearing the term radian for the first time. And if you left class still wondering “So, what are radians?,” don’t worry: we’ve got you covered. While the term may seem confusing at first, we’re here to help break exactly what radians are, and just how they can help you measure angles with ease.
What is a radian?
Simply put, a radian is another way to measure an angle instead of using degrees. You are merely switching the unit of measurement. It is like measuring your height in centimeters instead of inches.
This simple introduction will explain what radians are and how to calculate them. We don’t use radians in our everyday lives but you don’t need to feel intimidated by this unit of measurement.
Let’s begin with the basic parts of a circle:
An arc can refer to a full circle, a portion of a circle, or even longer than a circle. In this example, our arc is drawn as a full circle. The circumference is the length of that circle.
The radius (abbreviated to just “r”) is a straight line from the center of the circle to its edge. Be careful not to confuse “radius” with our similar-sounding friend “radians.”
As a rule, the radius of a circle can be used to calculate the circumference of a circle. The formula to calculate the circumference of a circle is:
2πr = circumference
Keep this formula in mind because it will return when we begin to calculate radians.
Units of measurement: Degrees
Degrees (abbreviated to °) are another unit of measurement, each counted as 1 of 360 equal slices of a circle. A full circle would be a total of 360°.
Why are circles divided into 360 parts? 360 is used for historical, not mathematical, reasons. The ancient Egyptians historically measured circles as a sum of 360 units because their measurement system was based on units of 60.
Despite being mathematically arbitrary, degrees are familiar to us. We use the language of degrees everywhere in everyday life. Idioms such as “a 180° change” describe moving in the completely opposite direction. Getting a “360° view” of something refers to a thorough perspective and understanding. Or the news may report on NASA’s 360° panoramic cameras.
In contrast, radians are pretty specific to higher level math. Don’t let the novelty worry you though. A radian is just another way to measure the same angle. For example, you can measure a circle as being 360° or as being about 6.28 radians.
How do you measure the radian?
A radian unit of measurement is based on the radius (which is why their names are similar). Take the length of the radius and measure out an arc. Imagine another line connecting the center of the circle to the end of that arc. The interior angle created by those two lines is 1 radius.
If you recall, the circumference of a circle = 2πr. The full circle’s angle = 2πradians.
How do you calculate radians from degrees?
The full circle’s angle can be measured as 360°. We just learned that it can also be measured as 2πradians. So, we can write this as:
360° = 2πRadians
Simplifying that equation gives us
180° = πradians
We can rearrange this formula to calculate the measurement we need.
180°/π = 1 radian
or put another way:
1° = π/180 radians
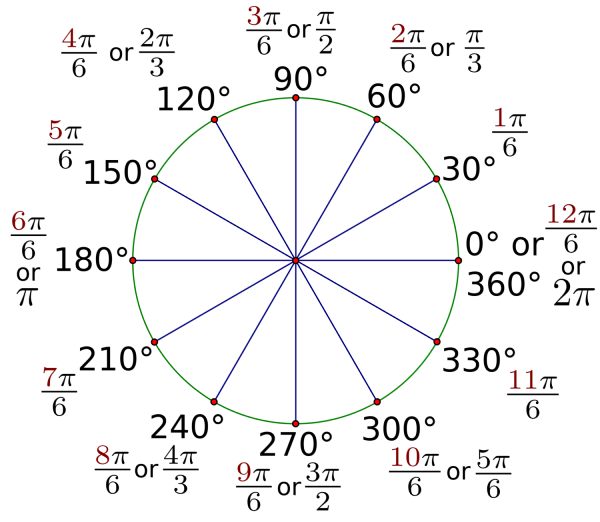
Sometimes you may see unit circles annotated like this:
There are far too many formulas there to memorize, and memorizing them all won’t make you any better at calculating radians As long as you remember the first formula we talked about—circumference = 2πr—you will be able to calculate between degrees and radians for the entire unit circle.
Final Thoughts
And there you have it! Now that you understand the basics of radians, you’re ready to start measuring angles. Prefer to work one-on-one with a tutor? Sign up to work with a free tutor on your time.
Not sure if you qualify for UPchieve’s free, on-demand, live tutoring? Head to our student sign-up page and check if your zipcode qualifies.
You can also check out our math series on algebra, expressions, geometry and our two part post on quadratic equations.