What is Geometry?
Are you ready to take your academic journey to the next level? We've got just the thing for you: UPchieve, your ultimate homework help companion! Sign up today for free!
Introduction
When you start any new class, it’s always a good idea to have a basic understanding of the subject you’re studying before you get deep into the work. This can be especially true as you get into the more advanced math and science, starting with algebra and geometry, and going straight through to calculus.
Today, we’re going to be tackling an explainer on geometry. By the end of this blog, you’ll be able to answer the question “What is geometry?” and you’ll even have an understanding of the basic principles to help you tackle geometry with ease!
What is a simple definition of geometry?
We’ll start with a basic definition. Geometry is defined as “a branch of mathematics that deals with the measurement, properties, and relationships of points, lines, angles, surfaces, and solids.”
Put even more simply, geometry is a type of math that deals with points, lines, shapes, and surfaces. When you hear “geometry,” thoughts of shapes, area, and volume probably come to mind—and that is precisely what geometry is!
Geometry, just like algebra, is built on a mathematical ruleset. In geometry, we refer to these rules as axioms, and there are 5 big ones that you should know.
What are the 5 axioms of geometry?
To get started, let’s take a look at what an axiom even is. In Euclidean Plane Geometry–which is the standard type of geometry taught in high school mathematics–axioms are used as the building blocks of problem-solving. Axioms used in high school geometry are based on the work of ancient Greek mathematician Euclid, and they allow us to establish certain mathematical truths from a few basic concepts. Euclid is considered the father of geometry, and his book The Elements is the earliest known textbook on this subject.
These 5 axioms of geometry are:
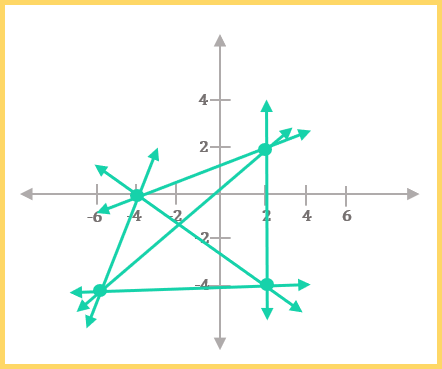
1. A straight line can be drawn between any two points.
Any two points in the same plane, or same flat space, can be connected by a straight line. This axiom is a fancy way of saying that you can “connect the dots.”
2. A straight line can be extended indefinitely.
Straight lines can go on and on—to infinity & beyond!
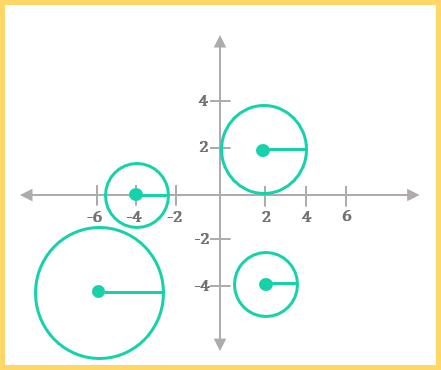
3. A circle can be made using any point as its center and a line segment as its radius.
This axiom says that you can make a circle around any point in a plane. Its radius will extend from the dot to the edge of the circle, forming a straight line.
4. All right angles are congruent.
We’ll cover congruence in another post, but for now, this just means that all right angles are the same. All right angles are exactly 90 degrees—no more, no less.
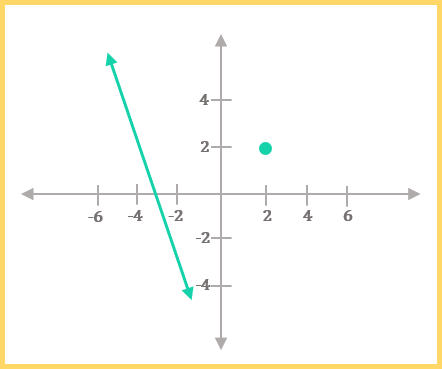
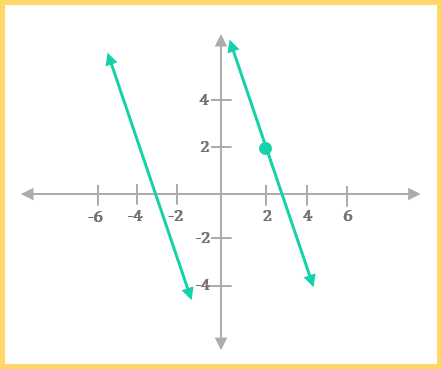
5. Parallel Postulate: given a straight line and a point (not on the line), there is always a second straight line through the point that will be parallel to the first line.
This one is a little less intuitive—pictures like the above help to clarify the statement. Essentially, this postulate just means that we can always draw a second line parallel to another line, assuming they’re in the same plane.
Final Thoughts on Geometry
Now that you can answer the question “What is geometry?” and know the five basic principles, you’re ready to start building on your knowledge! Many other theorems and properties can be built from these 5 axioms, just like how rules and equations are built on each other in algebra. Consider these 5 axioms your geometric foundation that will help you understand more complex problems down the line.
Need to ask a question about geometry, but don’t know where to go? Have a question about a specific axiom? Want some examples of how to apply these axioms? The tutors at UPchieve are here to help. You can connect with a tutor right now—it’s easier than saying Parallel Postulate three times fast!
Don’t need one-on-one help right now, but want to keep learning so you ace math this year? Check out our math series on algebra, expressions, radians, and our two part post on quadratic equations. Then make sure to download the UPchieve app so you can get free math homework help on the go, in as soon as five minutes!