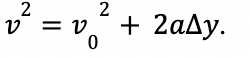How to Solve Kinematic Equations
If you're taking Physics, it won't be long before you start hearing about kinematic equations. To help you learn how to solve kinematic equations with ease, we’re going to cover some of the basic concepts behind them.
What are Kinematice Equations Used For?
Kinematic equations are the set of equations that that describe the motion of an object in either constant velocity motion (an 0 m/s/s acceleration) or constant acceleration. They’re used to help solve for the unknown in these instances.
The Concepts Behind Kinematic Equations
Equations and Units
Kinematics is a physics principle that studies movement. Specifically, 1D kinematics calculates motion of objects moving one way: up, down, or horizontally. We use three basic equations to find different aspects of moving objects.
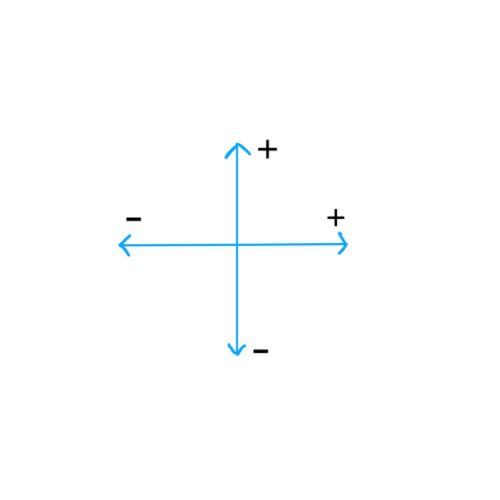
Signs
In physics, most numbers are vectors, which means they must either have a positive or negative sign. We usually follow the coordinate system to put signs on the numbers. For example, anything traveling right or up has a positive sign. Anything traveling left or down has a negative sign.
Quick Tips
Displacement is the distance between 2 points, not the total distance traveled.
Velocity at max height is 0 m/s2
Falling velocity is same as negative starting velocity at the same position.
Acceleration is usually a = -9.80 m/s2
Deceleration is acceleration with a negative sign
Time to reach max height = time to fall down
Practice
Problem solving strategy
Step 1: Draw it out! This will help you visualize the problem and help you check your answer at the end.
Step 2: List your givens! Write all your knowns and unknown from the problem on the diagram from step 1.
Step 3: Check out which equation you have to use. The right equation will contain all the variables from step 2.
Step 4: Plug and chug! To make your life easier, first solve for the unknown and then add in the numbers.
Step 5: Check to see if the answer makes sense by comparing it to the diagram.
Let’s practice!
Example 1
Bobby kicks a soccer ball straight up with a velocity of 10.0 m/s from a cliff’s edge that is 86.0 m high. a) How long does it take for the ball to hit the bottom of the cliff? b) What is the speed of the ball as it hits the ground? And c) how far did the soccer ball travel vertically?
Answer:
a) 5.33 s
b) -42.2 m/s
c) 96.2 m
Solution Key 1:
Step 1: Draw it out!
Step 2: List the knowns and unknowns.
Steps 3, 4, 5: Solve
For part a) we have to find t. The best equation to use would be:
Notice that we now use y, instead of x, since the ball is moving up and down in the y-axis. To solve for t, use the polynomial solver in your calculator or hand-solve using the quadratic formula.
We choose the positive answer because it makes more sense! So, it takes 5.33 s for the ball to hit the ground.
For part b) the best equation to use to find v is:
Velocity is negative because it is falling down! So the ball is traveling -42.2 m/s right before it slams into the ground.
For part c) we have to break up the distance traveled into 3 parts: distance to travel up, distance to travel back down to start point, and height of the cliff. Distance for the ball to travel up is the same distance to travel back down, and we find it using:
So, the total distance traveled is the sum of the distance to the top, the distance to the starting point, and the distance between the starting point and the bottom of the cliff.
5.10 m + 5.10 m + 86 m = 96.2 m
Key takeaways:
Acceleration will not always be given to you in the problem so you have to memorize that it is the acceleration due to gravity. Make sure to use the diagram to see what you have to solve for. Since the next problem can depend on the answer you got for the last problem, we must make sure that the last calculation was correct or we’ll get two wrong answers.
Here is an easier final example! 🤩
Example 2
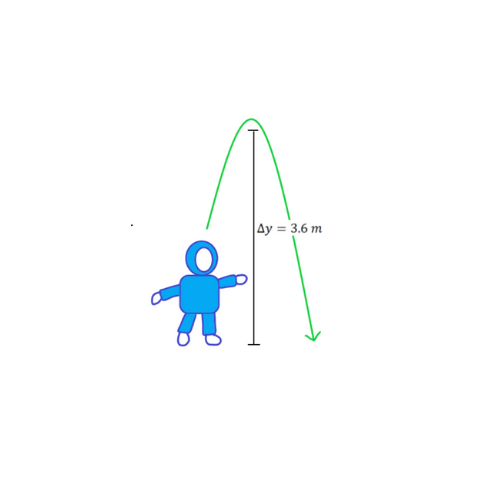
For exercise, Astronaut Shari bounces 3.6 m up in her space capsule where acceleration due to gravity is 9.76 m/s2. How long does it take her to come back to her original starting point?
Answer: 1.71 s
Solution Key 2
This problem requires two steps.
First, we have to find Shari’s original velocity. Second, we got to calculate the time.
As always, we draw a diagram and list our givens.
To find Shari’s starting velocity, we need to use the equations that have v, a, and Δy.
To find time, we use:
Key takeaways:
Displacement is not always the same thing as distance traveled!
Final Thoughts
Have a question about Physics? Sign up for UPchieve’s app to connect with an academic coach right now.